Склонение женского имени Юлия по падежам

Склонение женского имени Юлия по падежам: именительный, родительный, дательный,
винительный, творительный, предложный.
Удобный поиск склонений для слов, более 83451 слов в нашей базе.
Посмотрите обучающий видео урок
 как правильно склонять слова.

Падеж	Вопрос	Слово
именительный	Кто, что?	Юлия
родительный	Кого, чего?	Юлии
дательный	Кому, чему?	Юлии
винительный	Кого, что?	Юлию
творительный	Кем, чем?	Юлией
предложный	О ком, о чём?	о Юлии

Важно знать о склонении слов

Склонение существительных

Изменение имён существительных по падежам характеризуется изменением их окончаний, которые называются падежными формами. Всего в русском языке существует шесть падежей, каждый из которых имеет свой вспомогательный вопрос.

Для того, чтобы определить падеж имени существительного, нужно попробовать задать к нему один из вспомогательных вопросов.

Также существуют несклоняемые имена существительные, т.е. те, которые имеют во всех падежах одну и ту же форму. К несклоняемым относятся как имена нарицательные (например, «кофе» или «какао»), так и имена собственные (например, «Гёте»).

Как правило, несклоняемыми существительными оказываются слова, заимствованные из иностранных языков. Они могут относиться ко всем трем родам.

Склонение имен числительных

Склонение числительных не имеет единого образца, оно представлено несколькими типами:

1. Числительное один склоняется как прилагательное в единственном числе: один — одного (новый — нового).
2. Числительные от пяти до десяти и числительные на -дцать и -десят склоняются как существительные 3-склонения. У числительных на -десят два окончания, так как изменяются обе части: пятидесяти, пятьюдесятью.
3. Числительные сорок, девяносто, сто, полтора и полтораста, изменяясь по падежам, имеют только две формы: именительный и винительный падежи — сорок, девяносто, сто, полтора, полтораста; родительный, дательный, творительный, предложный падежи — сорока, девяноста, ста, полутора, полутораста.
4. Числительные от двухсот до четырехсот и от пятисот до девятисот склоняются по особому типу.
5. Собирательные числительные также склоняются по особому типу. Числительные оба, обе имеют два разных варианта склонения.
6. Простые порядковые числительные склоняются как прилагательные: первый (новый) — первого (нового). У сложных порядковых числительных только одно окончание. У составных порядковых числительных изменяется только последняя часть.
7. У дробных числительных при склонении изменяются обе части.

Склонение прилагательных

Склонение прилагательных – это изменение их по родам, падежам и числам.

Однако не все прилагательные изменяются и по родам, и по числам, и по падежам. Краткие прилагательные не изменяются по падежам, а прилагательные в форме простой сравнительной степени вообще не склоняются.

Для того, чтобы правильно склонять имена прилагательные, нужно знать их падежные вопросы в обоих числах.

Важно понимать, что окончание прилагательного можно проверить окончанием вопроса.

Видеоурок. Склонение имен существительных по падежам

Склонение других имён

Эсмеральда

Этери

Юзефа

Эмма

Эрнестина

Эмилия

Эля

Эрика

Эльмира

Цецилия

---

---

Ещё никто не оставил комментария, вы будете первым.

Алфавитный указатель

А

Б

В

Г

Д

Е

Ж

З

И

Й

К

Л

М

Н

О

П

Р

С

Т

У

Ф

Х

Ц

Ч

Ш

Щ

Э

Ю

Я

---

Имя Юлия — склонение по падежам, значение имени

• И. п. Юлия
• Р.п. Юлии
• Д.п. Юлии
• В.п. Юлию
• Т.п. Юлией
• П.п. Юлии

Юлия — женское имя, по происхождению римское.
Вариант написания имени транслитом (латиницей): Yuliya

Значение имени

См. ИУЛИЯ. Пышная, сноп.»Кудрявая», «Пушистая», «Из рода Юлиев» (лат.)
С необузданной фантазией, обидчивая и ранимая девочка. В настроении заметны сильные перепады, когда веселая, резвая и шумная Юленька становится вдруг без особой причины вялой и апатичной.В таком состоянии лучше всего оставить девочку в покое: пройдет время, и она снова станет прежней. Ее трудно переспорить, до последнего стоит на своем, неохотно признает свою ошибку.Несколько пуглива, не любит смотреть фильмы ужасов, не переносит вида крови.
Взрослая Юлия запаслива, бережлива, хорошо готовит. Чего только нет в ее кладовых!Семье, хозяйству, благополучию родных Юлия уделяет почти все свое время; работа, профессиональный рост ее интересуют мало, поэтому у коллег часто складывается впечатление о Юлии, как о человеке с ленцой.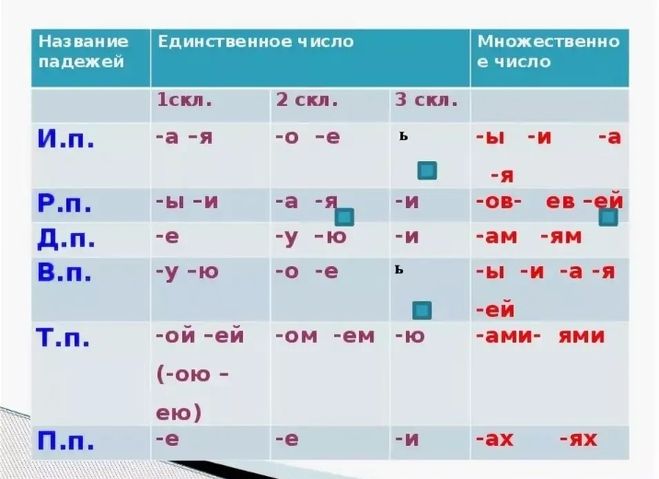 Юлия удачлива в браке, двери ее дома всегда открыты для друзей и родственников. Гости к Юлии ходят охотно, она не скупа, любит поболтать с подружками, немного посплетничать, искренне радуется успехам друзей, не завистлива.Мешает Юлии упрямство, которым она отличается с детства. Она не будет следовать чужим советам даже в тех случаях, когда знает, что они вполне разумны. Эта черта характера не дает Юлии находить общий язык с матерью и свекровью, именно поэтому она предпочитает жить с ними врозь.Многие Юлии — страстные книголюбы, чтение — их любимое занятие. Они не позволят скучать мужу, всегда внесут разнообразие в семейную жизнь. Муж обычно любит Юлию и во всем ей подчиняется.
Самозабвенно любит своих детей.Именины:

31 (18) мая и 29 (16) июля — мученица Иулия дева.

Нумерология имени

Число души: 5.
Число имени 5 означает свободу и независимость. «Пятерки» редко слушают советов со стороны, они привыкли опираться на свой собственный опыт. Они склонны попробовать, нежели обдумать. «Пятерки» любят приключения и путешествия, сидеть на месте не в их характере! Они – игроки и авантюристы, жажда риска и азарт сопутствуют всему их жизненному пути. Родная стихия «пятерок» — торг, в любых торговых делах мало кто сравнится с «пятерками». Стоит помнить, что «пятерки» всеми силами избегают ответственности.

Число скрытого духа: 1
Число тела: 4

Знаки

Планета: Венера.
Стихия: Воздух и вода, тепло-влажность.
Зодиак: Телец, Весы.
Цвет: Зеленый, желто-синий, розовый.
День: Пятница.
Металл: Медь, бронза.
Минерал: изумруд, аквамарин, берилл, хризолит, сапфир, сердолик.
Растения: Барвинок, мелисса лекарственная, незабудка, венерин башмачок, нехищные орхидеи, ирис, цветная капуста.
Звери: Голубь, бык, кошка, кролик, тюлень, лань.

Комментарии посетителей

Julius/Julia/Julium, AO — Latin is Simple Online Dictionary

Перейти к основному содержанию род/семейство

а/ юлианцы

Метаинформация

A/O — Склонение

Формы

• Положительные
• 9001 1
• Сравнительная степень
• Превосходная степень

Сг.	Мужской	Женский	Средний
Ном.
Ген.
Дат.
Согл.
Voc.
Абл.
Пл.	Мужской	Женский	Средний
Ном.
Ген. Дат.
Согл.
Voc.
Абл.

Примеры предложений

В текстовом корпусе не найдено ни одного вхождения этого слова.

Найдите еще фрагменты латинского текста в библиотеке Latin is Simple

Пометить как спам

Дополнительная информация

Вставить эту запись на свой сайт

Похожие слова

• …

Добавить похожие слова / Это слово не похоже на другие

Словарные группы :

Найдите больше латинских слов с помощью функции расширенного поиска.

«-» является сокращением для «данной формы не существует»

Для студентов

Переводите текст прямо сейчас?

Анализ латинских предложений!

Анализ вашего текста слово за словом и обнаружение ACI, NCI, P.C. и Абл.Абс.!

… или, может быть …

Готовишься к завтрашнему повторению словарного запаса?

Дайте шанс единственному тренажеру словарного запаса, который просит латинские основные части!

Комплексные и рациональные числа · Язык Julia

Julia включает предопределенные типы как для комплексных, так и для рациональных чисел и поддерживает все стандартные математические операции и элементарные функции над ними. Преобразование и продвижение определены таким образом, что операции с любой комбинацией предопределенных числовых типов, будь то примитивные или составные, ведут себя должным образом.

Глобальная константа im связана с комплексным числом i , представляющим главный квадратный корень из -1. 2.5
2,7292
-2 + 0им
юлия> 1 + 3/4им
1.0 — 0.75im

Обратите внимание, что 3/4im == 3/(4*im) == -(3/4*im) , так как буквальный коэффициент связывает сильнее, чем деление.

Предусмотрены стандартные функции для работы со сложными значениями:

 julia> z = 1 + 2im
1 + 2им
julia> real(1 + 2im) # действительная часть z
1
julia> imag(1 + 2im) # мнимая часть z
2
julia> conj(1 + 2im) # комплексное сопряжение z
1 - 2им
julia> abs(1 + 2im) # абсолютное значение z
2.23606797749979julia> abs2(1 + 2im) # квадрат абсолютного значения
5
julia> angle(1 + 2im) # фазовый угол в радианах
1.1071487177940904 

Как обычно, абсолютное значение ( абс ) комплексного числа равно его расстоянию от нуля. abs2 дает квадрат абсолютного значения и особенно полезен для комплексных чисел, поскольку позволяет избежать извлечения квадратного корня. angle возвращает фазовый угол в радианах (также известный как функция аргумента или аргумента ). Полный спектр других элементарных функций также определен для комплексных чисел:

 юлия> sqrt(1im)
0,7071067811865476 + 0,7071067811865475им
юлия> sqrt(1 + 2im)
1,272019649514069 + 0,7861513777574233им
юлия> cos(1 + 2im)
2,0327230070196656 - 3,0518977991517997им
юлия> exp(1 + 2im)
-1,1312043837568135 + 2,4717266720048188им
юлия> sinh(1 + 2im)
-0,4890562590412937 + 1,4031192506220405im 

Обратите внимание, что математические функции обычно возвращают действительные значения при применении к действительным числам и комплексные значения при применении к комплексным числам. Например, sqrt ведет себя по-разному при применении к -1 по сравнению с -1 + 0im , хотя -1 == -1 + 0im :

 julia> sqrt(-1)
ОШИБКА: DomainError с -1.0:
sqrt вернет сложный результат только при вызове со сложным аргументом. Попробуйте sqrt (комплекс (x)).
Трассировки стека:
[...]
юлия> sqrt(-1 + 0im)
0.0 + 1.0im 

Обозначение буквенных числовых коэффициентов не работает при построении комплексного числа из переменных. Вместо этого умножение должно быть явно записано:

 юлия > а = 1; б = 2; а + б*им
1 + 2im 

Однако это , а не . Вместо этого используйте более эффективную комплексную функцию для создания комплексного значения непосредственно из его действительной и мнимой частей:

 julia> a = 1; б = 2; комплекс (а, б)
1 + 2im 

Эта конструкция позволяет избежать операций умножения и сложения.

Inf и NaN распространяются через комплексные числа в действительной и мнимой частях комплексного числа, как описано в разделе «Специальные значения с плавающей запятой»:

 юлия> 1 + инф*им
1.0 + Инф*им
Юлия> 1 + NaN*im
1.0 + NaN*im 

Джулия имеет рациональный тип числа для представления точных отношений целых чисел. Рационалы строятся с помощью оператора //:

 julia > 2//3
2//3 

Если числитель и знаменатель рационального числа имеют общие делители, они приводятся к наименьшим слагаемым, так что знаменатель неотрицательен:

 julia> 6//9
2//3
юлия>-4//8
-1//2
юлия> 5//-15
-1//3
юлия>-4//-12
1//3 

Эта нормализованная форма отношения целых чисел уникальна, поэтому равенство рациональных значений можно проверить, проверив равенство числителя и знаменателя. Стандартизированный числитель и знаменатель рационального значения можно извлечь с помощью функций числителя и знаменателя :

 julia> numerator(2//3)
2
юлия> знаменатель(2//3)
3 

Прямое сравнение числителя и знаменателя, как правило, не требуется, поскольку стандартные арифметические операции и операции сравнения определены для рациональных значений:

 юлия> 2//3 == 6//9
истинный
юлия> 2//3 == 9//27
ЛОЖЬ
юлия> 3//7 < 1//2
истинный
юлия > 3//4 > 2//3
истинный
юлия> 2//4 + 1//6
2//3
юлия> 5//12 - 1//4
1//6
юлия> 5//8 * 3//12
5//32
юлия> 6//5 / 10//7
21//25 

Рациональные числа можно легко преобразовать в числа с плавающей запятой:

 julia> float(3//4)
0,75 

Преобразование из рационального числа в число с плавающей запятой соблюдает следующее тождество для любых целых значений a и b , за исключением двух случаев b == 0 и a == 0 && b < 0 :

 julia> a = 1; б = 2;
julia> isequal(float(a//b), a/b)
true 

Допустимо построение бесконечных рациональных значений:

 julia> 5//0
1//0
юлия> х = -3//0
-1//0
Юлия> typeof(x)
Rational{Int64} 

Попытка построить NaN рациональное значение недействительна:

 julia> 0//0
 ОШИБКА: ArgumentError: неверный рациональный: ноль (Int64) // ноль (Int64)
 Трассировки стека:
 [.